Στο Acta Eruditorium τον Ιούνιο του 1696 (ίσως το πρώτο επιστημονικό περιοδικό) εμφανίστηκε ένα σημείωμα από τον διάσημο Ελβετό επιστήμονα Johann Bernoulli με τίτλο «Ένα νέο πρόβλημα που οι μαθηματικοί καλούνται να επιλύσουν», που το διατύπωνε ως εξής:
Έστω δυο δεδομένα σημεία Α και Γ σε ένα κατακόρυφο επίπεδο.
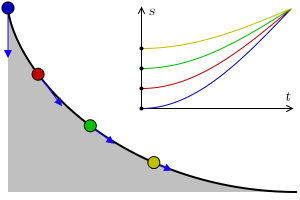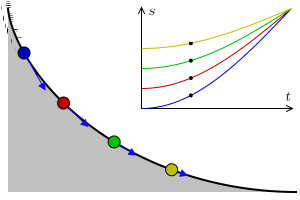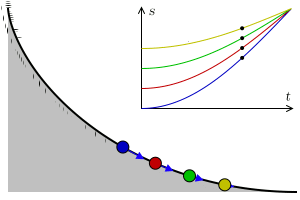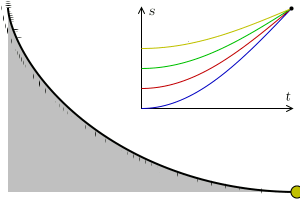
Να βρεθεί η καμπύλη την οποία πρέπει να διαγράψει ένα υλικό σημείο σημείο που κινείται στη διαδρομή ΑΓ υπό την επίδραση του βάρους του, έτσι ώστε, ξεκινώντας από το Α, να φτάσει στο Γ στον ελάχιστο χρόνο.
Πολλοί μαθηματικοί έλυσαν το πρόβλημα του Johann Bernoulli, όπως ο Lebniz, Jakob Bernoulli (ο αδελφός του Johann) και ίσως ίδιος ο Newton καθώς μια ανώνυμη λύση που στάλθηκε αποδίδεται σ’ αυτόν.
Όλοι κατέληγαν στο συμπέρασμα ότι η ζητούμενη «βραχυστόχρονη» είναι η κυκλοειδής καμπύλη. Η κυκλοειδής είναι η τροχιά που διαγράφει κάποιο συγκεκριμένο σημείο ενός κύκλου που κυλίεται χωρίς να ολισθαίνει, πάνω σε μια ευθεία γραμμή.
Το όνομα της κυκλοειδούς (ως καμπύλης που σχετίζεται με τον κύκλο) εμφανίστηκε για πρώτη φορά στις εργασίες του Γαλιλαίου σαν επεξηγηματικό παράδειγμα. Την ανακάλυψαν ξανά στη Γαλλία οι Mersenne, Roberval, Descartes και Pascal και την βάφτισαν roulette.
Οι κορυφαίοι μαθηματικοί του 17ου αιώνα μελέτησαν πλήρως την κυκλοειδή καμπύλη προσδιορίζοντας τις εξισώσεις των εφαπτομένων της, τα εμβαδά των χωρίων που περικλείονται από αυτήν και τον άξονα των τετμημένων, τα μήκη των τόξων της, κ.ο.κ.
Και στη συνέχεια εμφανίστηκε άλλη μια έκπληξη. Aποδείχθηκε τελικά ότι αυτή, και όχι – όπως έγραφε ο Γαλιλαίος – κύκλος, έχει την εξής ιδιότητα: ένα σώμα που ολισθαίνει κατά μήκος της χωρίς τριβές ταλαντώνεται με περίοδο που δεν επηρεάζεται από την αρχική του θέση. Αυτή η ιδιότητα του ταυτόχρονου (ή του ισόχρονου) της κυκλοειδούς ανακαλύφθηκε από τον Huygens και προκάλεσε ενθουσιασμό. Ο ίδιος ο Huygens έγραψε ότι «η ανακάλυψη [αυτής] της ιδιότητας της κυκλοειδούς συνιστά τον πλέον ποθητό καρπό, ένα είδος αποκορυφώματος της διδασκαλίας του Γαλιλαίου για την πτώση των σωμάτων».
Ο ενθουσιασμός όμως για την κυκλοειδή καμπύλη με το πέρασμα του χρόνου άρχισε να μειώνεται καθώς τελικά δεν ήταν το «εργαλείο» που θα έδινε απαντήσεις και σ’ άλλα θεμελιώδη προβλήματα της Φυσικής.
Η «απαξίωση» της κυκλοειδούς καμπύλης σήμερα είναι ακόμα μεγαλύτερη και όλο πιο σπάνια την συναντάει κανείς σε βιβλία φυσικής.
Η κυκλοειδής καμπύλη αποτελεί λύση της εξίσωσης Friedmann
Κι όμως η κυκλοειδής καμπύλη έχει περισσότερες εφαρμογές.
Και η εντυπωσιακότερη απ’ όλες να είναι το γεγονός ότι αποτελεί λύση της εξίσωσης Friedmann που περιγράφει την χρονική εξέλιξη του μεγέθους του σύμπαντος.
Η εξίσωση Friedmann προκύπτει από την επίλυση των εξισώσεων πεδίου της Γενικής Θεωρίας της Σχετικότητας, θεωρώντας την ομογενή και ισότροπη μετρική Robertson-Walker.
Στην εξίσωση περιέχεται ο παράγοντας κλίμακας R(t), ο οποίος περιγράφει την χρονική εξέλιξη του μέγεθους του σύμπαντος ή πιο συγκεκριμένα την χρονική εξάρτηση κάθε τυπικού μήκους, όπως για παράδειγμα την απόσταση μεταξύ δυο γαλαξιών:
$ \left( \dfrac{dR}{dt} \right)^{2} = \dfrac{8}{3} \dfrac{\pi G \rho_{0}R^{2}_{0}}{R(t)}-kc^{2}$ (1)
όπου G η σταθερά της παγκόσμιας έλξης, ρ0 και R0 οι σημερινές τιμές της ενεργειακής πυκνότητας του σύμπαντος και του παράγοντα κλίμακας αντίστοιχα.
Ο γεωμετρικός παράγοντας k παίρνει τις τιμές k=0, +1 και -1, που καθορίζουν την γεωμετρία και την εξέλιξη του σύμπαντος.
Στην περίπτωση που k=+1 παρατηρούμε ότι η υπάρχει χρονική στιγμή t κατά την οποία ο παράγοντας κλίμακας R(t) εμφανίζει ένα μέγιστο.
Η μέγιστη τιμή $Rmax$ υπολογίζεται πολύ εύκολα θέτοντας στην εξίσωση Friedmann, $dR(t)/dt=0$,
$R_{max}=\dfrac{8 \pi G \rho_{0} R^{3}_{0}}{3c^{2}}$
Αντικαθιστώντας στην αρχική εξίσωση (1) έχουμε:
$ \dfrac{dR}{dt}=c \sqrt{\dfrac{R_{max}-R(t)}{R(t)}} \Rightarrow \int_{0}^{R} \frac{\sqrt{R}}{\sqrt{R_{max}-R}}dR = ct$
Το τελευταίο ολοκλήρωμα υπολογίζεται κάνοντας τον μετασχηματισμό $R=R_{max}\sin^{2}(\theta/2)$, παίρνοντας τελικά
$t(\theta)=\dfrac{R_{max}}{2c}(\theta - \sin \theta)$ και $R(\theta)=\dfrac{R_{max}}{2}(1- \cos \theta)$
Οι δυο αυτές εξισώσεις αποτελούν την παραμετρική έκφραση της κυκλοειδούς καμπύλης που περιγράφει το κλειστό σύμπαν (k=+1).
Στο παραπάνω σχήμα βλέπουμε την εξέλιξη του R(t) για την περίπτωση του ανοιχτού σύμπαντος (k=-1, με τιμή παραμέτρου πυκνότητας Ω0=0.5), την περίπτωση του επίπεδου (k=0 και Ω0=1) και την περίπτωση που εξετάστηκε εδώ, το κλειστό σύμπαν (k=+1, με Ω0=2).
Στην περίπτωση του κλειστού σύμπαντος το σύμπαν διαστέλλεται φθάνοντας σε μια μέγιστη «ακτίνα» Rmax και στη συνέχεια συστέλλεται μέχρι την Μεγάλη Σύνθλιψη (το αντίθετο της Μεγάλης Έκρηξης). Και η κυκλοειδής καμπύλη περιγράφει την «ακτίνα» αυτού του σύμπαντος συναρτήσει του χρόνου.